Partial differential equations are foundational to modern science; they describe the physics of physical phenomena from weather and ocean currents to general relativity and quantum mechanics.
If you are anything like me, just the very mention of partial differential equations (PDEs) brings back memories of dusty blackboards, migraines, and a general feeling of “why are we even trying to understand these things, they’re never going to help us in the real world”. (Yes I know, not a great attitude).
In my rather poor defense, since studying them in an elective engineering module at university (ironic hey), we have in fact never since been reacquainted. In my mind at least, they remain a very abstract concept.
One thing I did manage to learn about PDEs, however, is they are very difficult to solve; and as it turns out, the general scientific community also shares this opinion. So why then, are we still investing time trying to solve them?
Partial differentials and the secrets they hold
Part of the answer lies in the remarkable way these mathematical equations are able to model changes over space and time. This unique property makes them especially good for describing many of the physical phenomena we observe in our world, including sound and heat transfer, diffusion, electrostatics, electrodynamics, fluid dynamics, elasticity, general relativity, and quantum mechanics.
By understanding these phenomena, and solving the PDEs that describe them, opens the door to being able to predict, at any given point in time, what will happen next, and what happened before.
Sound familiar? DEVS tech thriller
This ability to model our world and have AI “solve” the mathematical equation was the very story behind the BBCs gripping thriller, DEVS. If you want to truly see the art of the (im?)possible, this is a worthwhile investment of a box-set-credit.
“The universe is deterministic, and always the result of a prior cause”
PDEs in the real world
Bringing us back to reality, let’s explore some real-world applications of PDEs.
One particularly useful class of partial differentials is the Navier–Stokes equations. Founded independently in the early 1800s by French engineer Claude-Louis Navier and English Physicist Sir George Gabriel Stokes, this set of equations describe how the velocity, pressure, temperature, and density of a moving fluid are related. In other words, they describe the motion of a fluid (including air).
Navier–Stokes equations are applied to many real-world applications:
- Modeling the movement of air around wings and other surfaces during the design of aircraft and cars.
- Studying blood flow in medicine.
- The efficient design of power stations, modeling flow rates, and heat transfer.
- Analysis of pollution, weather, and ocean movements.
- And many others…
Differential & Partial Differential Equations explained
At this point, it may help the reader (it certainly helped the writer) to understand PDEs in simple terms. Feel free to skip this section, but I found these examples helpful, and if you want to see these and others, read some great explanations of derivatives and partial derivatives on MathsIsFun.com.
Let’s start with a Differential Equation. This is an equation with a function and one or more of its derivatives:
y + dy/dx = 5x
In this example, the function is y and its derivative is dy/dx
MathsIsFun helps to understand dy/dx (the derivative):
“Think of dN/dt as how much the population changes as time changes, for any moment in time”
This (trivial) example helps further illustrate this.
A partial derivative is a form of derivate where one variable remains constant, like in this example:
PDEs and Artificial Intelligence
Few would have foreseen any overlap between PDEs and the modern field of artificial intelligence. However, mathematicians started looking to modern AI for help because at the heart of solving partial differentials, is a highly complex and computationally intensive problem.
Historically, this has required powerful super-computers to crunch calculations. But, even with powerful compute on tap, these “traditional” mathematical approaches have produced limited results.
How Deep Learning is Solving the Puzzle
For the first time, modern advances in AI, specifically in the field of Deep Learning, have enabled PDEs to be solved to a degree of accuracy, and generalisation, not seen before. This has been made possible by the groundbreaking research at Caltech, the California Institute of Technology.
Researchers at Caltech applied a class of neural networks that used Fourier Neural Operators, to produce a highly optimised neural net for solving PDEs.
The results are astonishing:
- A new level of accuracy for predicting future/past dynamics
- Highly generalizable, and can be applied (without retraining) to solve many classes of PDEs, including Navier–Stokes
- 1,000 times faster than traditional (mathematical) solvers
Professor Anima Anandkumar is also the Director of AI Research at NVIDIA. Follow Anima Anandkumar on Twitter.
Predicting the future (you have to start somewhere)
In this simulation, you can see how the predicted movement of the fluid by their model (right) exactly matches the actual movement observed (middle). The model predicted this from a point in time (left).
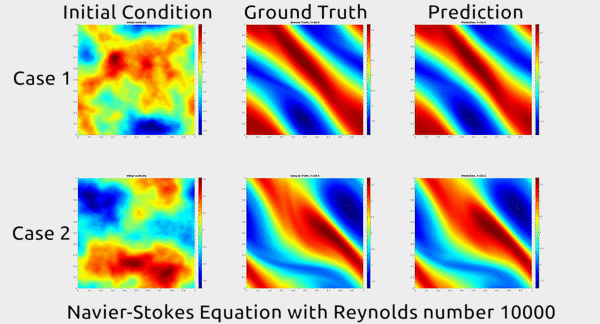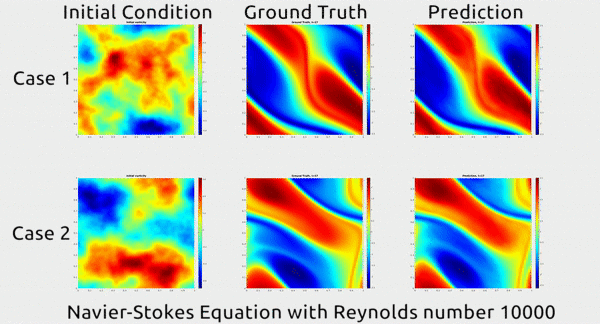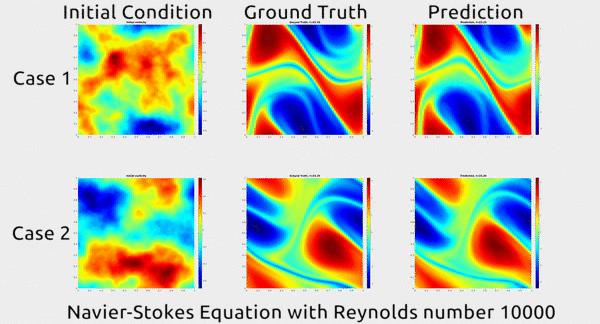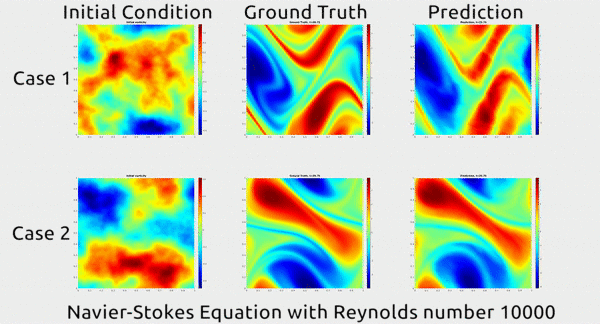
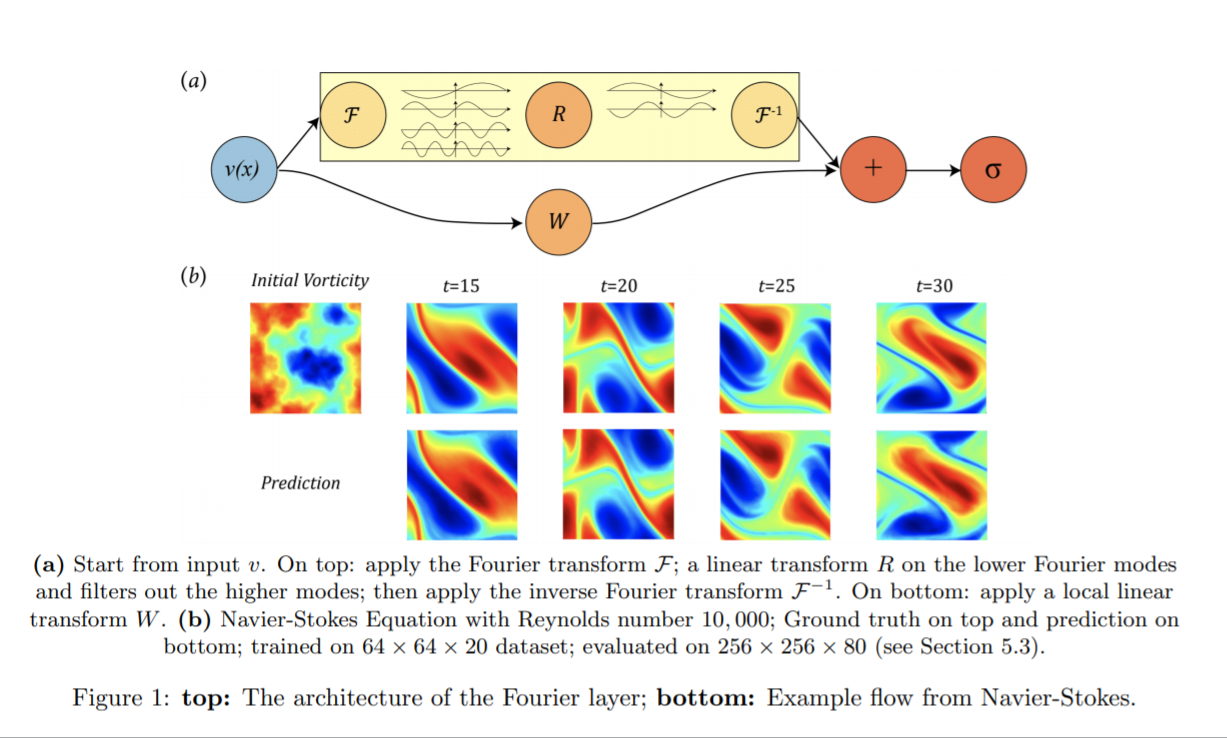
In the above simulation, a (challenging) Reynolds number of 10,000 was used. The Reynolds number is a ratio of a fluid’s inertial force to its viscous force, and a number over 4,000 is generally described as “turbulent”, where liquid molecules execute unpredictable movements. 10,000 therefore, explains the seemingly random movement seen in the simulation (taken from this paper).
How did they do it?
“The classical development of neural networks has primarily focused on learning mappings between finite-dimensional Euclidean spaces. Recently, this has been generalized to neural operators that learn mappings between function spaces. For partial differential equations (PDEs), neural operators directly learn the mapping from any functional parametric dependence to the solution. Thus, they learn an entire family of PDEs, in contrast to classical methods which solve one instance of the equation.”
This excerpt is taken from Caltech's’ research paper, released October 20, 2020.
Convolutional Neural Network
In the paper, they start by discussing the limitations of traditional AI approaches which used deep Convolutional Neural Networks (CNNs). These models rely on finite-dimensional Euclidean spaces and require extensive tuning and modification depending on the PDE and scenario being analysed.
FEM-Neural Network
They move on to discuss an improved, but still sub-optimal approach using a finite element method (FEM) based neural network. This approach is designed to model one specific instance of the PDE, and therefore is more generalised than the CNN, reducing the need for tuning and modification. It also produced more accurate predictions. However, it require retraining as coefficients in the problem set are changed, and also the underlying PDE must be known.
Neural Operators
Introduced in late 2019, these enabled a neural network to have infinite-dimensional operators. The neural operator only needs to be trained once, a clear advantage over earlier approaches. Obtaining a solution for a new instance of the parameter requires only a forward pass of the network, alleviating the major computational issues incurred in Neural-FEM methods. Lastly, the neural operator requires no knowledge of the underlying PDE, only data.
However, this wasn’t the silver bullet the researchers were hoping for:
“Thus far, neural operators have not yielded efficient numerical algorithms that can parallel the success of convolutional or recurrent neural networks in the finite-dimensional setting due to the cost of evaluating integral operators. Through the fast Fourier transform, our work alleviates this issue. ”
Researchers at Caltech, the California Institute of Technology
Fourier transform
The Fourier transform is frequently used in spectral methods for solving differential equations since differentiation is equivalent to multiplication in the Fourier domain.
"We build on these [research] works by proposing a neural operator architecture defined directly in Fourier space with quasi-linear time complexity and state-of-the-art approximation capabilities."
Researchers at Caltech
Caltech’s neural network used a novel deep learning architecture that made use of these Fourier transform operators. The astonishing performance of the network in part stems from its ability to learn mappings between infinite-dimensional spaces of functions; the integral operator is instantiated through a linear transformation in the Fourier domain as shown in Figure 1 (a).
Conclusion
This is a groundbreaking leap forwards. We see it having a positive impact in ethical areas, such as modeling climate change and ocean currents to help in marine biology and conservation. Predictive aerodynamics, for example in aircraft, cars, and lorries, could boost efficiency and help as we move from combustion to electric as our choice of power.
Next steps
1. Read Caltech’s research paper
2. Learn more about Ancoris Data, Analytics & AI